k-means Clustering: an Explainer

A brief, example-driven explainer of k-means clustering.

Today I’ll be demonstrating how \(k\)-means clustering works through a variety of examples.

\(k\)-means clustering is a statistical procedure to classify observations (data corresponding to a single object) into categories, without a target. In machine learning, this would be considered an unsupervised learning technique. Each category will have a mean across the one or more categories, and each observation is classified into one of \(k\) (the number of categories) categories based on which group whose mean to which it is closest. Since the categories may be poorly formed at first, the categories are found in an iterative approach.

For example, suppose we had weights, lengths, and body fat percentages of 30 golden retrievers. We know there are 15 males and 15 females in the data, but the data don’t say whether any specific dog is male or female. However, we understand that male dogs tend to be larger and leaner. In this case, we could perform \(k\)-means clustering with \(k = 2\) categories. We would expect there to be a category representing males which would have a larger mean weight, larger mean length, and smaller body fat percentage, and guess that those dogs are male. In this case, there would be no guarantee that the golden retrievers are correctly classified as male or female, nor that there would be 15 in each group. It could very well be the case that a female is especially large and lean and could be classified as male. From an intuitive perspective, this would be like seeing a golden retriever from a distance, noticing that it is an especially large and lean dog and anticipating it to be male.

In the following post, I’ll be demonstrating \(k\)-means clustering when given either one, two, or three variables with which to classify observations. The 2D and 3D examples both involve colors with visually compelling interpretations, while the 1D example shows an easy-to-understand numerical example.

1-Dimensional Example

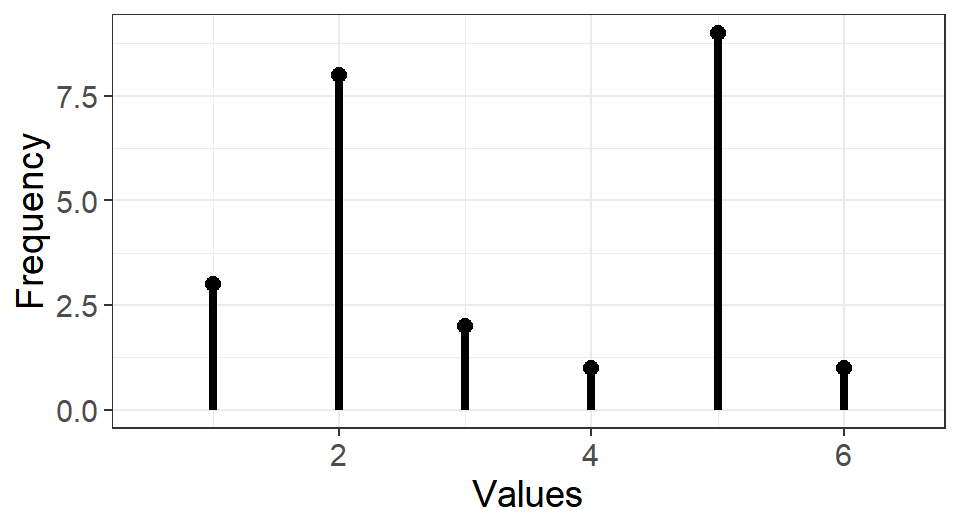
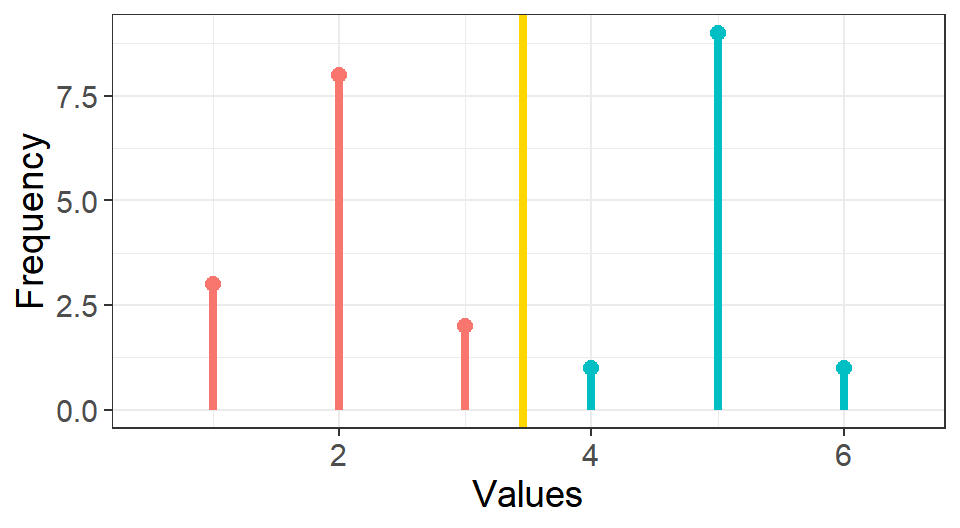
Suppose that we have a vector of data, \(\bf{x} =\) \(<1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6>\) (plotted above), and would like to perform \(k\)-means clustering with \(k=2\) clusters (two clusters or two groups) on \(\bf{x}\). When we do, it separates the vector into two groups in such a way that each group consists of the most similar values to each other. Below, we see that the means of the two groups (red and blue) are 5 and 2, giving a dividing or discriminating line (yellow) at 3.46. That is, anything larger than the yellow line is classified to be “large” and anything smaller the yellow line is classified to be “small.”

Aside: Colors as Data

We can represent colors with red, green, and blue values (like on a CRT TV) in a single pixel. A pixel in a picture, then, can be represented in the form \(<x, y, R, G, B>\), where \(x\) and \(y\) represent the location of the pixel, while \(R, G,\) and \(B\) represent the red, green, and blue values. A single color value (say, red), is conventionally represented with 8 bits and can thus take on \(2^8 = 256\) different values, which we map to \(0\) to \(255\). Oftentimes, you’ll see see these stored in hexadecimal, which is a base 16 number system (that is, we use the conventional base 10 digits: \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9\), and, having run out of symbols we recognize as numbers, proceed to letters: \(A, B, C, D, E, F\)). So, an 8-bit value (which has \(2^8\) possibilities) can be represented by two hexadecimal values (\(2^8 = 2^4 \cdot 2^4\)). For example, the number \(175\) in base 10 (AKA decimal) can be represented as \(AF\) in base 16 (AKA hexadecimal). Bonus: \(175\) in base 10 can be represented as \(10101111\) in base 2 (binary). I digress. As an example, consider the color yellow, which can be represented as #FFFF00 (that is, \(FF \rightarrow 255\) and \(00 \rightarrow 0\) – maximum red and green, minimum blue).

2-Dimensional Example

So, we have a single pixel, \(<x, y, R, G, B>\). For this 2-dimensional example, let’s set the green value to \(128\) and allow the \(x\) and \(y\) dimensions to be the same as the \(R\) and \(B\) dimensions. That is, if \(R = 0, B = 4\), then the pixel is plotted at \(x = 0, y = 4\). We have \(<x = R, y = B, R, G = 128, B>\), so only \(R\) and \(G\) vary (2 dimensions). Below, we have 64 by 64 evenly spaced pixels plotted of this type – this is the 2 dimensional data we will be classifying:

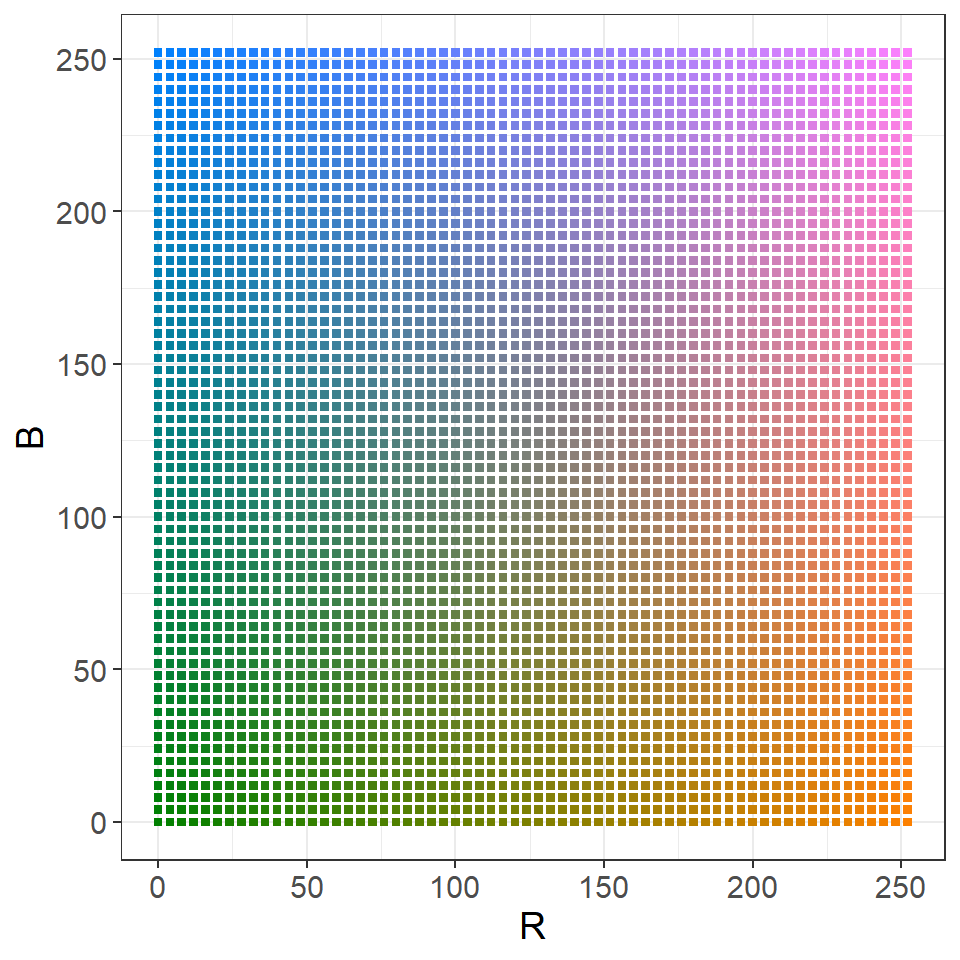
\(k\)-means Clustering

Now, let’s perform \(k\)-means clustering on these pixels with \(k = 2, ..., 9\) clusters. For example, let \(k = 2\). This means that we will be using two clusters, or two groups. The method will find the two groups that are the most similar and classify each pixel into one of these two groups. When it classifies pixels into groups, it finds the mean of each group (in this case, that’s a mean vector in the \(R\) and \(G\) dimensions, e.g., \(<\bar{R}, \bar{B}>\)). I’ll represent each of the resulting clusters with the mean color of that cluster in the plot below. But first, some details:

In this case, kmeans broke our data into two equal-sized clusters (this is not a requirement, but because all of the \(R\) and \(B\) values are equally-spaced, we get equal-sized clusters) of size 2048. The mean vectors (centroids) of the two clusters are \(<\bar R = 190, \bar B = 126>\) and \(<\bar R = 62, \bar B = 126>\). Now, we plot the resulting clustering:

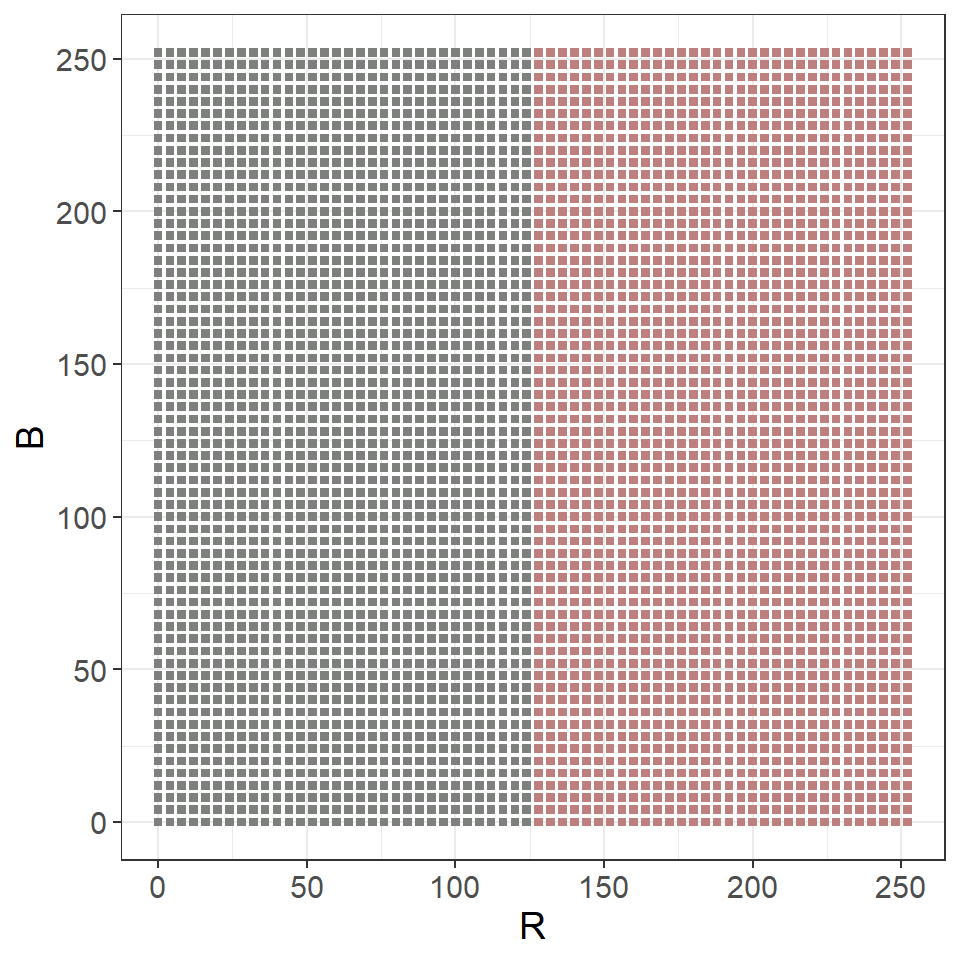
As you can see, these clusters are brown-ish (or gray-ish) and not terribly representative of the original data. But, if we had to reduce all of the pixels to one of two colors, this is the most representative reduction.

Now, an \(R\) function, cluster_plotter, to generalize this process to any \(k\):

Show code

cluster_plotter = function(data = RGcolor, k, pixelsize = 1.2){
  set.seed(1234) # to keep results consistent

  clustering = kmeans(select(data, R, B), centers = k)

  cluster_means = clustering[[2]] %>% as.data.frame() %>% 
    add_rownames(var = "cluster") %>% 
    mutate(across(c(cluster, R, B), as.integer)) %>% 
    rename(Red = R, Blue = B)
  
  RGcolor2 = data %>% 
    mutate(cluster = clustering[[1]]) %>% 
    left_join(y = cluster_means, by = "cluster") %>% 
    mutate(hexcolor = RGBtohex(R = Red, G = G, B = Blue, round.by = 1))
  
  plotted = RGcolor2 %>% 
    ggplot(aes(x = R, y = B)) + 
    geom_point(color = RGcolor2$hexcolor, size = pixelsize, pch = 15) + 
    theme(axis.text = element_blank(), axis.ticks = element_blank(),
      axis.title = element_blank())
  
return(plotted)
}

Clustering \(k = 2, ..., 9\)

Now, let’s look at how effective \(k\)-means clustering is with two, three, … or nine clusters:

We can see that as we increase the number of clusters, the classifications get closer and closer to the original data.

Clustering \(k = i^2; i = 2, ..., 9\)

So, what if we increase the number of clusters at a quadratic rate? That is, we attempt with four, nine, … or 81 clusters:

When we get to \(k = 81\) clusters (bottom right plot), the resulting clustering is nearly indistinguishable from the very first 2-D plot.

3-Dimensional Example

Now, let’s work with the Simpsons couch gag as data:

Figure 1: Generic Simpsons Couch Gag (Looper)

We can convert this to data (e.g. each pixel is represented as \(<x, y, R, G, B>\) and is a row in our data). Below are 5 sample pixels from this 563 by 1000 pixel image (that’s 563,000 rows of data!).

x	y	R	G	B	color
485	605	30	54	20	#1e3614
368	601	51	141	185	#338db9
235	249	220	120	141	#dc788d
373	129	223	120	135	#df7887
439	850	8	144	130	#089082

Now, we can perform clustering on this data. Let’s let \(k = 8\). Below are five sample rows from this clustering, where the final five columns show the clustered representation.

Original Data						Clustered Data
x	y	R	G	B	color	cluster	Red	Green	Blue	hexcolor
118	277	221	121	142	#dd798e	8	216	116	135	#d87487
470	719	166	71	0	#a64700	2	147	62	14	#933e0e
558	422	165	40	153	#a52899	6	164	74	115	#a44a73
171	280	220	120	141	#dc788d	8	216	116	135	#d87487
323	60	221	121	142	#dd798e	8	216	116	135	#d87487

Finally, let’s re-plot the clustered data to re-form the original picture (using only eight (!) colors):

It’s remarkable how much we can do with just eight colors, although there are obvious differences between the original image and this (Homer’s facial hair, Marge’s dress, etc). Also, many of the colors lean towards brown or gray since they’re the average of several colors (recall the 2D \(k = 2\) example). Let’s do it again with \(k = 50\) (50 colors):

Aside from the pixelation issues on the lines (if you’ve ever zoomed into a rasterized image, you’ll see that lines that are supposed to be black are actually a blend of black and the colors around it) there are only a couple of minor color differences. For example, the gradation at the top of the image is not smooth (presumably this screenshot is from a streaming service which put a slight overlay on top to indicate a pause screen).

For more from me on \(k\)-means Clustering…

See my blog posts where I demonstrate creating generative art (remixing the Simpsons couch gag) and have some fun with my process.